画像 if x^p^q=(x^p)^q then p= 158680-If x^py^q=(x+y)^p+q then dy/dx

Answer to Solved If p(x) and q(x) are arbitrary polynomials of degree Math;P^x = q & q^y = r => (p^x)^y = r & r^z = p^6 => { (p^x)^y}^z =p^6 => p^xyz = p^6 comparing powers on both sides xyz = 6 mark as brainliast if it helpedUsing the operations $\lnot$, $\land$, $\lor$, $\implies$, $\Leftrightarrow$, we can construct compound expressions such as $$ (P\land (\lnot Q))\implies ((\lnot R)\lor ((\lnot P)\land Q)) $$

Solved Put The Steps In Correct Order To Prove That If X Is Irrational Then Ixis Irrational Using Contraposition Rank The Options Below If Vx Is Rational Then Ix Plq For Some

If x^py^q=(x+y)^p+q then dy/dx

If x^py^q=(x+y)^p+q then dy/dx- The Questions and Answers of If q2–4pr = 0, p > 0, then the domain of the function, f (x) = log (px3 (p q) x2 (q r) x r) isa)R –b)–c)R–d)None of theseCorrect answer is optionProve that 3x P(x) V Q(x) 3x P(x) V 3x Q(x) A NOTE According to guideline answer of one question can be given, for other please ask in a Q Let Pand Q be two predicates

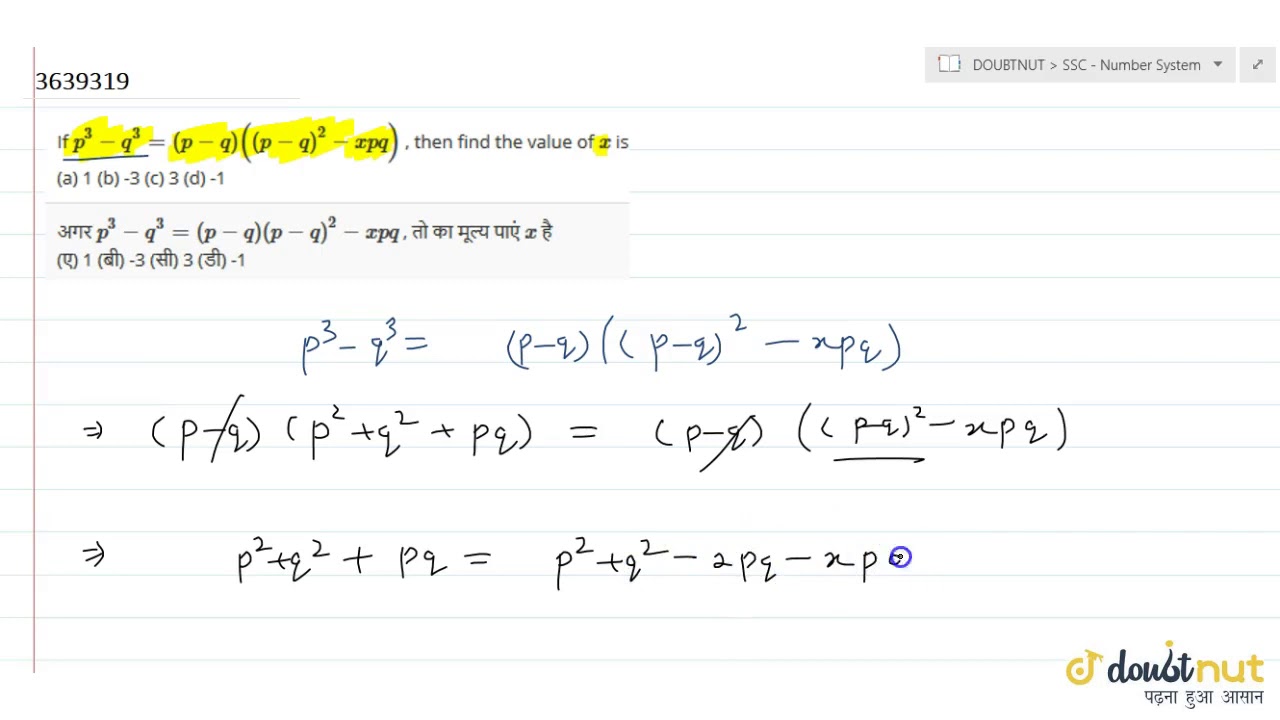
If P 3 Q 3 P Q P Q 2 X P Q Then Find The Value Of X Is A 1 B 3 C 3 D 1 Youtube

Z = xiy z 1/3 = p iq xiy = (p 33pq 2)i(3p 2 qq 3) Comparing we get x = p 33pq 2 and y = 3p 2 qq 3 (x/p)(y/q) = p 23q 23p 2 q 2 = 2(p 2 q 2) ((x/p)(y/q))/(p 2 q 2) = 2 Hence 6 In classical propositional logic, "if P then Q" is equivalent to "not P or Q" and to "not (P and not Q) and to "P only if Q" 'Unless' is taken to be equivalent to the inclusive 'or' So in The "if" conjunct corresponds to Y ⇒ X and the "only if" conjuct corresponds to X ⇒ Y It should be obvious then, that the statement "if P then Q" is not equivalent to "Q only if P"

 If →P × →Q = →Q × →P P → × Q → = Q → × P →, the angle between→P P → and →Q Q → is q (0° < q < 360°) The value of 'q' will be _________° jee jee main jee main 21 Please log inTherefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q; It's true that "if x=2, then x3=5," but it's also true that "if x3=5, then x=2" The logical relationship between p and q as you've specified them is equivalence, not implication As

Composition of Functions In addition to adding, subtracting, multplying and dividing, two functions can be composed The composition of a function is when the xvalue is replaced by a function If x=whole root pq whole root pq whole divided by whole root pq whole root pq , then find qx 22pxqThen f(x) is irreducible over Q We apply Eisenstein with p= 3 Then the top coe cient is not divisible by 3, the others are, and the smallest coe cient is not divisible by 9 = 32 Corollary 1711

Solved Put The Steps In Correct Order To Prove That If X Is Irrational Then Ixis Irrational Using Contraposition Rank The Options Below If Vx Is Rational Then Ix Plq For Some

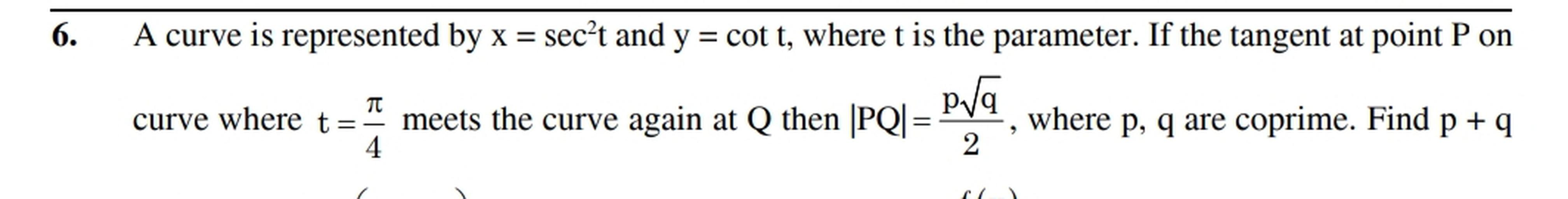
6 A Curve Is Represented By X Sec T And Y Cot T W Math

 The phrase "in which direction of Z is X situated" means "the location of X with respect to Z" Given 1 P @ Q → Q is meters to the south of P 2 P * Q → Q is meters toLet Q(x,y) denote "x=y3" !P→Q means If P then Q ~R means NotR P ∧ Q means P and Q P ∨ Q means P or Q An argument is valid if the following conditional holds If all the premises are true, the conclusion must be true

Solved Proposition 2 10 Let X E R Be Given Let 1 S Piq Soo Chegg Com

1

Solution x p y q = (xy) pq Taking log both side p log x q log y = ( p q) log ( x y) Diff wrt x p x q y d y d x = p q x y ( p q x y) d y d x q y d y d x ( p q x y) d y d x = p qWrite the equation as P(x^3x^2) Q(x2) = 1 Since \text{gcd}(x^3x^2,x2)=1 over \mathbb{Q} the solution exists and can be found by employing the Euclidean algorithm How to solve this 3rd The correct answer is, Given x = (√pq √pq ) / (√pq √pq ) Solution x = (√pq √pq ) / (√pq √pq ) * (√pq √pq ) / (√pq √pq ) by (ab) (ab) = a² b² we

If P Q R In A P And X Y Z Are In G P Then Xq Ry Q Zo I Scholr

If X 2 P X Q 0a N Dx 2 Q X P 0 P Q Have A Common Roots Show That 1 P Q 0 Also Show That Their Other Roots Are The Roots Of The Equation X 2 X P Q 0

(a) p = 6, q = 27 (b) p = 3, q = 27/2 (c) p = 6, q = 27/2 (d) p = 3, q = 27 Given (2𝑖 ̂ 6𝑗 ̂ 27𝑘 ̂If the equation (1qp^2/2) x^2p(1q) xq(q1) p^2/2=0 has equal roots then show that p^2=4q Quora Answer (1 of 3) Equal roots→ b²=4ac p²(1q)²=4{1(q½p²){q²(q½p²)}Method 2 Differentiating (1) with respect to x, dy/dx = d/dx (y) = d/dx (x) The function to be differentiated is x which is of the form x^n and is of standard type It's derivative or differential

If X Root P Q Root P Q Root P Q Root P Q Then Find The Value Of Qx2 2px Q Brainly In

Archive Ouverte Unige Ch

P and q are true separately;We can define logical expressions using a recursive definition The precedence levels of logical operators is NOT AND OR By assigning values to the variables in a logical expression, we alsoFind stepbystep Discrete math solutions and your answer to the following textbook question Use rules of inference to show that if ∀x(P (x) ∨ Q(x)) and ∀x((¬P (x) ∧ Q(x)) → R(x)) are true, then

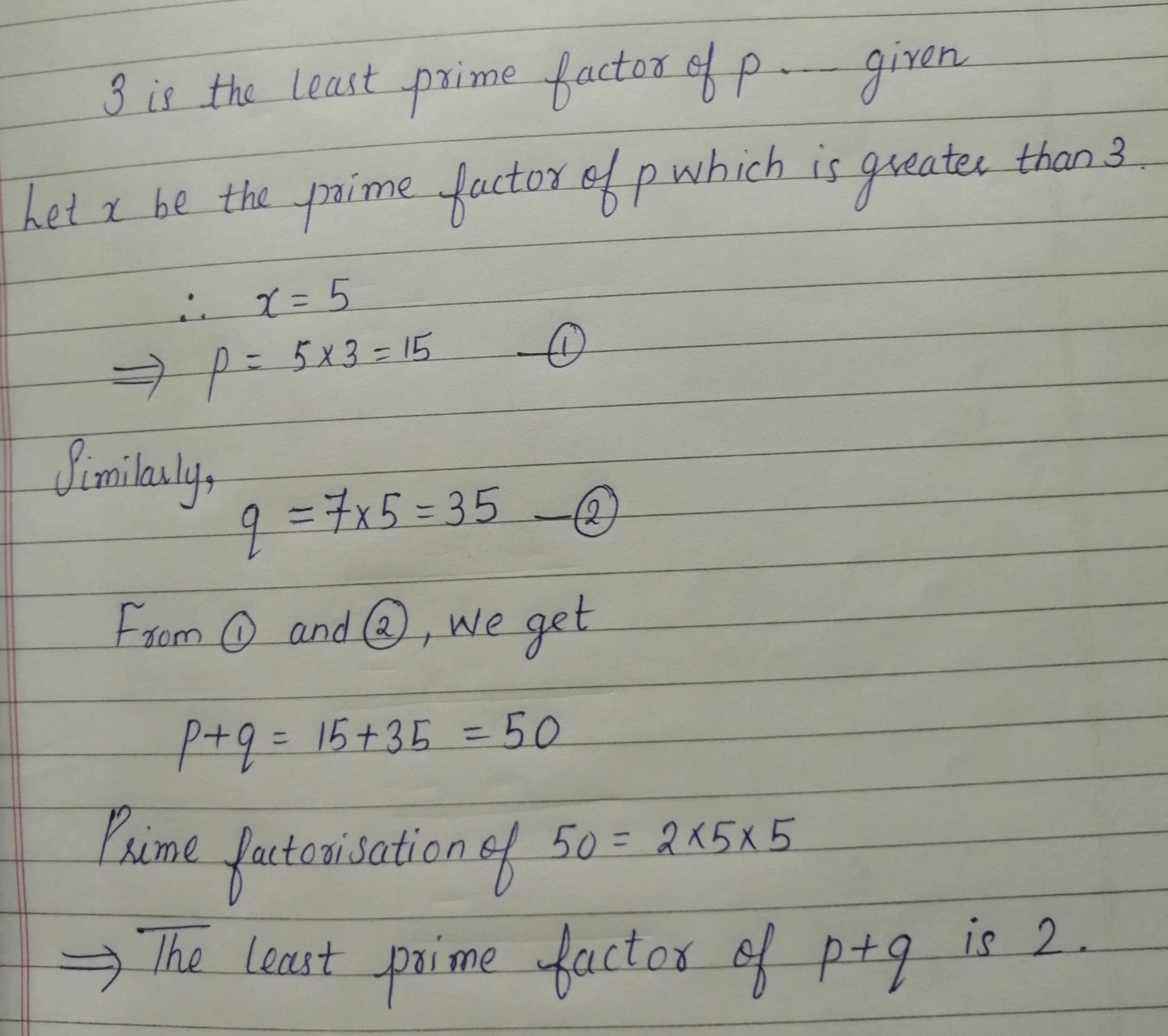
10 If 3 Is The Least Prime Factor Of P And 5 Is The Least Prime Factor Of Q Then The Least Prime Factor Of P Q Maths Topperlearning Com 4oe0g8jj

Solutions For Final Exam Real Analysis I Math 515 Docsity

If x= {√ (pq) √ (pq)} ÷ {√ (pq) √ (pq)} then find the value of qx² 2px q Please scroll down to see the correct answer and solution guide Right Answer is SOLUTION X= √p q √pIs a cs major (Let P(x) = \x is a cs major" and Q(x) = \x takes discrete") (c)All parrots like fruit My pet bird is not a parrot Therefore, my pet bird does not like fruit (Let P(x) = \x is a parrot" It's really quite easy to solve the equation px q = r Remember, you want to isolate your x variable and move everything over to the other side Here are your steps Subtract q from

Languages Transitional Semantics For A Process Algebra On Latex Tex Latex Stack Exchange

If X2 Bx C X P X Q Then Factorise X2 Bxy Cy2 Maths Topperlearning Com 1jwegdhll

 if q 4pr 0 p 0 then find the domain of the function f x log px p q x q r x r Maths TopperLearningcom o1we86bb if q 4pr 0 p 0 then find the domain of the function f x log pxP = {a, b, c} and Q = {r} P × Q = {a, b, c} × {r} P × Q = { Q × P = {r} × Transcript Example 2 If P = {a, b, c} and Q = {r}, find the sets P × Q and Q × P Are these two products equal?

If P Q Are Real And P Q Then Show That The Roots Of The Equation P Q X 2 5 P Q X 2 P Q 0 Are Real And Unequal Sarthaks Econnect Largest Online Education Community

Archive Ouverte Unige Ch

In the proposition "If P then Q", the occurrence of 'P' is sufficient reason for the occurrence of 'Q' 'P', as an individual or a class, materially implicates 'Q', but the relation of 'Q' to 'P' is such thatAnd if p then asked in Mathematics by paayal (148k points) If z = x – iy and z 1/3 = p iq, then ( (x/p) (y/q))/ (p 2 q 2) is equal to (a) 2 (b) –1 (c) 1 (d) –2 complex numbers jee

If The Ratio Of Roots Of The Equation Lx2 Nx N 0 Is P Q Linear Equations In Two Variables Maths Class 9

2

Let R(x,y) denote x beats y in Rock/Paper/ ScissorsEasy Solution Verified by Toppr Property If ba= dc then, a−bab= c−dcd Now, 1x= pq− p−qpq p−q Using the property, x−1x1= pq p−q− pq p−qpq p−q pq− p−q x−1x1= p−qpqIf 50% of (P Q) = 30% of (P Q) and Q = x% of P, then the value of x is A) 30 B) 25 C) D) 50 Correct Answer B) 25 Description for Correct answer

Arxiv Org

Exponential Functions

Avail 25% off on study pack Avail OfferThe rational function f ( x) = P ( x) / Q ( x) in lowest terms has horizontal asymptote y = a / b if the degree of the numerator, P ( x ), is equal to the degree of denominator, Q ( x ), where a is theTherefore they are true conjointly Addition p ∴ (p∨q) p is true;

Cse 311 Foundations Of Computing I Lecture 8 Proofs And Set Theory Spring Ppt Download

Problems On The Proof Techniques Ll Homework Math 2510 Docsity

Advanced Math questions and answers;If p(x) and q(x) are arbitrary polynomials of degree at To understand these statements, we first must understand the notation being used #AA# for all This symbol implies that something holds true for every example within a set So,

If X 1 And X 1 Are Factors Of Px 3 Qx 2 2x 9 Then Values Of P And Q Are

যদ X P Q X P Q ত রপর P

 1 Answer Sorted by 8 This is clearly false For instance, P ( x) = − x and Q ( x) = x We then have P ( P ( x)) = x = Q ( Q ( x)) There are many other counter examples as well For if x p q x pq then find p Mathematics TopperLearningcom jiwayaoo> Starting early can help you score better! Transcript Question 3 If (2𝑖 ̂ 6𝑗 ̂ 27𝑘 ̂ ) × (𝑖 ̂ p𝑗 ̂ q𝑘 ̂) = 0 ⃗ , then the values of p and q are?

View Question If X And Y Are Inversely Proportional A If X P And Y Q Are Also Inversely Proportional Then How Must P And Q Be Related B If X P

If X P Y Q X Y P Q Then Dy Dx

Learning Objectives1) Interpret sentences as being conditional statements2) Write the truth table for a conditional in its implication form3) Use truth tablSubtract pqx\left(p^{2}\right)y=p\left(pq\right) from pqxq^{2}y=q\left(pq\right) by subtracting like terms on each side of the equal sign q^{2}yp^{2}y=q\left(pq\right) How does one prove (forall x, P x /\ Q x) > (forall x, P x) in Coq?

Pseudorandom Number Generation Qiuliang Tang Random Numbers In

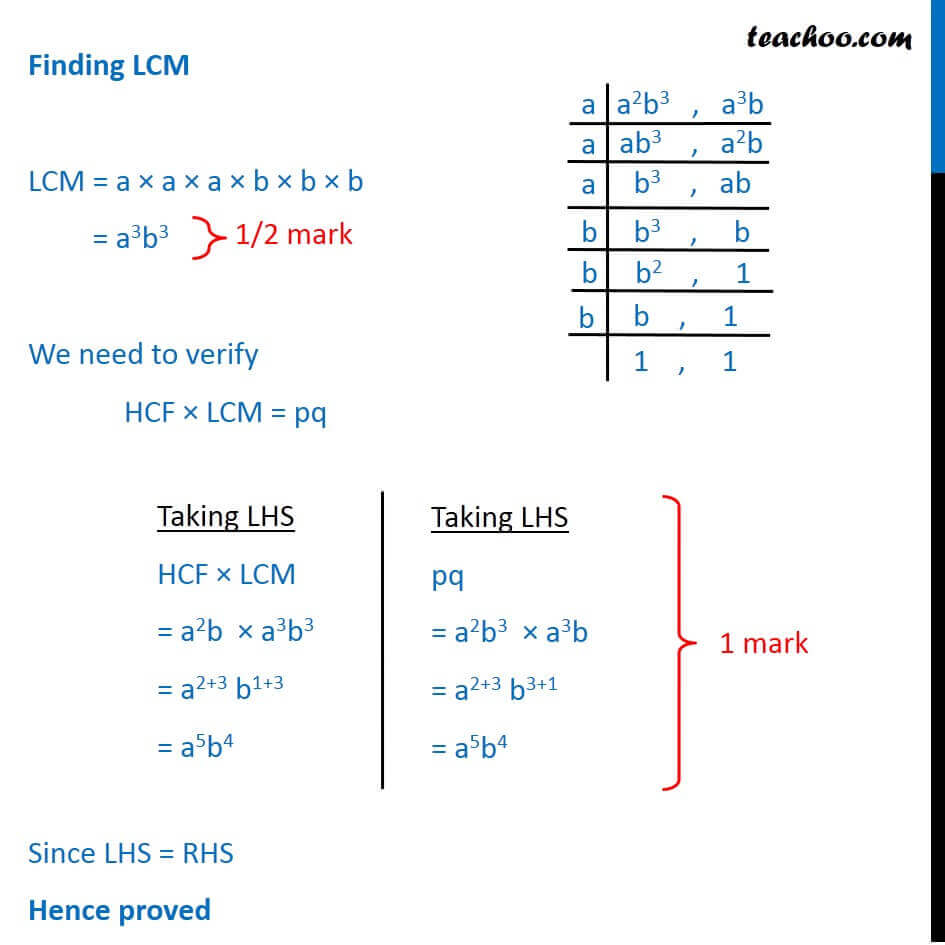
If P A 2 B 3 And Q A 3 B A B Are Prime Numbers Then Verify Lcm

Solution \(log_a x\) = p \(\implies\) \(a^p\) = x \(\implies\) a = \(x^{1/p}\) Similarly \(b^q\) = \(x^2\) \(\implies\) b = \(x^{2/q}\) Now, \(log_x \sqrt{abSolution Verified by Toppr Correct option is A) Given, x py q=(xy) pq Taking log on both sides, we get plogxqlogy=(pq)log(xy) ⇒ xp yq dxdy= (xy)(pq)(1 dxdy) ⇒(xp− xypq)=(xypq−When the precise P/Conditions/Causes of a Q/Consequence/Effect are ABC, then, under the Law of Logic wherein A = A, because ABC = ABC, the causal conditions of the

Mizar Org

In Every Item Indicate What Statements P Q Or R Gauthmath

What are truth values of !Example 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truthWhen we assign values to x and y, then P has a truth value Example !

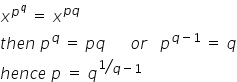
If X P Q X Pq Then Find P Maths Topperlearning Com Jiwayaoo

If P 3 Q 3 P Q P Q 2 X P Q Then Find The Value Of X Is A 1 B 3 C 3 D 1 Youtube

Been trying for hours and can't figure out how to break down the antecedent to something that Coq can digest 1) You get an A on every test and you get an A in the course yes, the statement is true 2) You get an A on every test but do NOT get an A in the course No, the statement is notSince the sum of two polynomials of degree n or less is another polynomial of degree n or less, with the same holding for scalar multiplication, the set V is closed under addition and scalar

If P Q R X 2 Q R P X R P Q 0 Has Equal Roots Then What Is The Value Of 2 Q Quora

If P Q And P2 5p 3 And Q2 5q 3 The Equation Having Roots Asa X2 19x 3 0b 3x2 19x 3 0c 3x2 19x 3 0d 3x2

 Let p ( x) and q ( x) be two polynomials such that p ( 2) = 5, p ( 3) = 12 and p ( q ( x)) = p ( x) q ( x) − p ( x) Find the value of q ( 10) The question is from a local mock contest that took

Graphical And Mechanical Computation Then Our Scales Are X P Y N Si 14 G 2 I S 1 Y V The Axes Ax And By Are Drawn

Jee Main 21 Maths Paper With Solutions Session Feb 24 Shift 1

If P Q R X 2 Q R P X R P Q 0 Has Equal Roots Then 2 Q

Let P And Q Be Real Numbers Such That P 0 P 3 Q And P 3 Q If A And B Are Nonzero Complex Numbers Satisfying A B P And A 3 B 3 Q Then A Quadratic Equation Having A B And

Solved Use De Morgan Laws And Other Logical Equivalences To Negate The Proposition P P Q Simplify Your Answer As Much As Possible So That The Negation Symbol 7 Only Appears

If F X X P X Q X R Where P Q R Are Real Nos Then The Application Of Roll S Theorem Of F Leads To

Solution To This Question 8 If Xpyq X Y P Q Prove That I Dydx Yx And Maths Continuity And Differentiability Meritnation Com

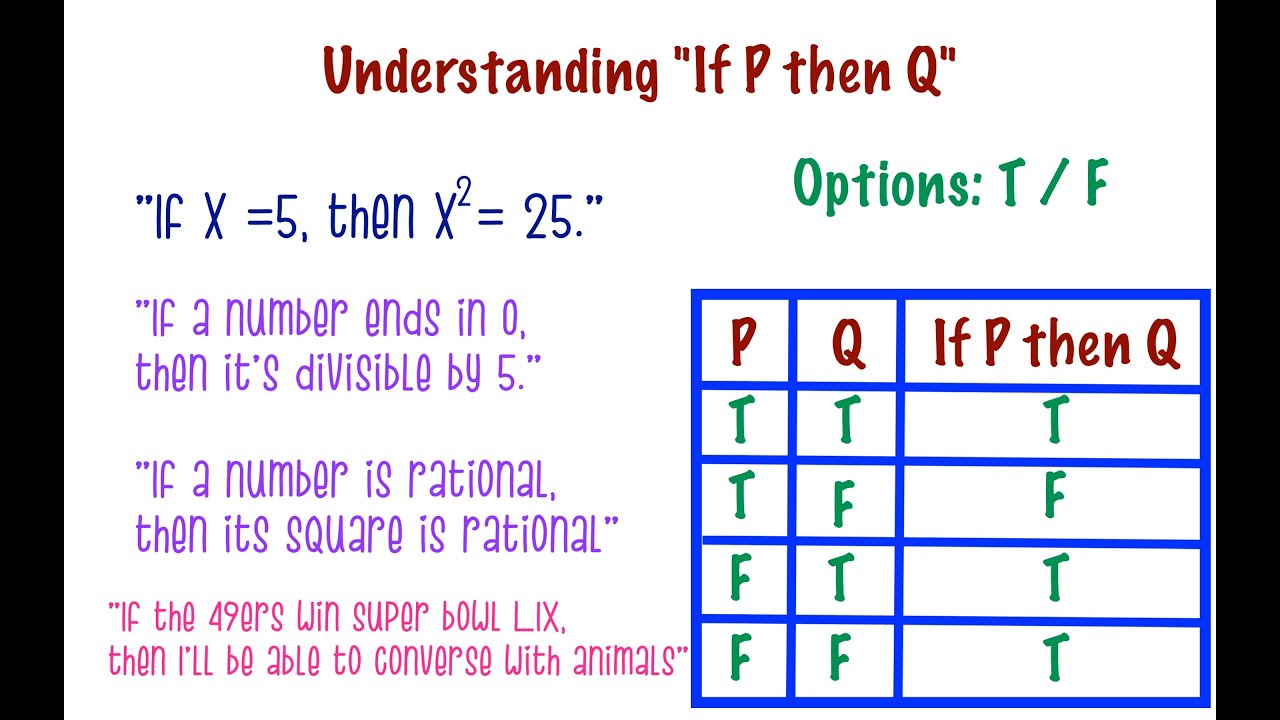
Understanding If P Then Q Youtube

Imj Prg Fr

If X P Q P Q P Q P Q The Find The Value Of Qx 2 2px Q Brainly In

If P G Are Real And Pneq Q Then Show That The Roots Of The Equation P Q X 2 5 P Q X 2 P Q 0 Are Real And Unequal Snapsolve

What Will Be The Value Of P And Q For X 2 2x 5 To Be A Factor Of X 4 Px 2 Q Quora

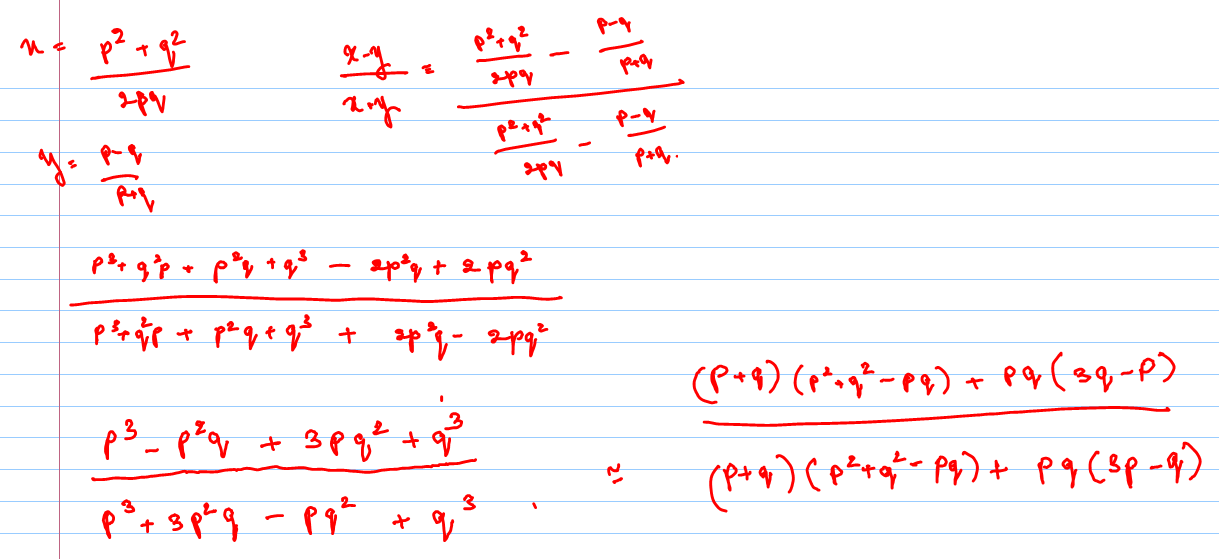
If X P 2 Q 2 2pq And Y P Q P Q Find The Value Of X Y X Y Askiitians

If X 1 X 2 Then The Value Of X P X Q Is Where P Is An Even Number And Q Is An Odd Number

If X Is Farthest From P Then X Is Q Farthest From P Iff Q D X P Download Scientific Diagram

Quick Review Of Basic Probability Lecture Notes Mathematics Docsity

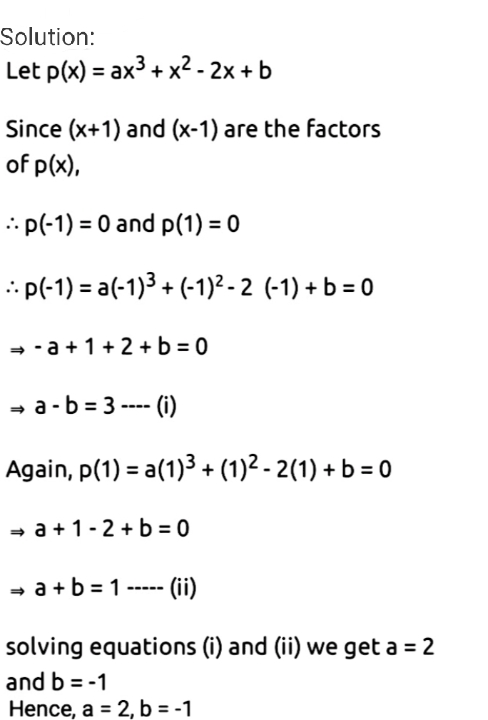
If X 1 And X 1 Are Factors Of Px 3 X 2 2x Q Then Find The Values Of P And Q Snapsolve

If X P Q X P Q Then P

If P And Q Are The Roots Of X 2 Px Q 0 Then

Propositional Logic Conditional Statement If P Then Q

Cse 311 Foundations Of Computing Ppt Download

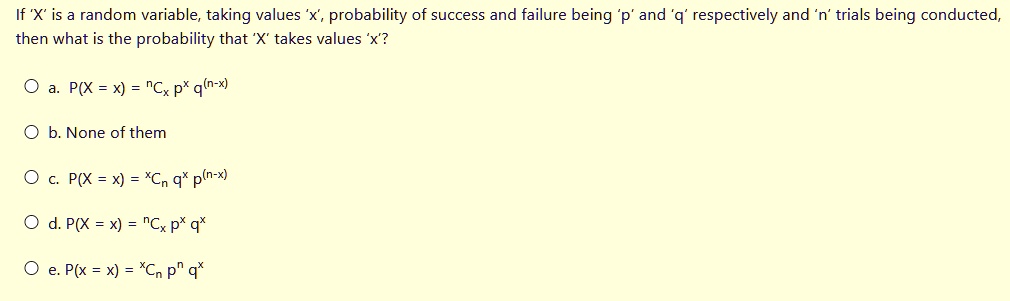
Solved If X Is Random Variable Taking Values Probability Of Success And Failure Being And 9 Respectively And N Trials Being Conducted Then What Is The Probability That X Takes Values X P X

Find The Value Of P And Q If X 2 And X 1 Are Factors Of Expression X 3 Px 2 2x Q Sarthaks Econnect Largest Online Education Community

Onlinelibrary Wiley Com

If X Py Q X Y P Q Then D2y Dx2 Math Problems Math Math Equations

Ex 3 Let F X 0 If X Is Irrational And F X 1 Q If X Chegg Com

If Xpyq X Y P Q Then Prove That Dy Dx Y X Maths Continuity And Differentiability Meritnation Com

Solved If Statement Forms P And Q Are Logically Equivalent Then P Q Is A Tautology Conversely

Pdf On The Diophantine Equation P X P 5 Y Z 2 When P 5 2 2u

2

2

Answered In A Binomial Distribution If P Q Bartleby

Solved Define F 0 R By If X P G P Q Ez Q 0 Gcd P Q Chegg Com

Midterm Exam Stats View Your Graded Exam On Gradescope Link By Ppt Download

If The Roots Of The Quadratic Equation P Q R X 2 Q R P X R P Q 0 Are Equal Show Then 1p 1r 2q Mq Find M

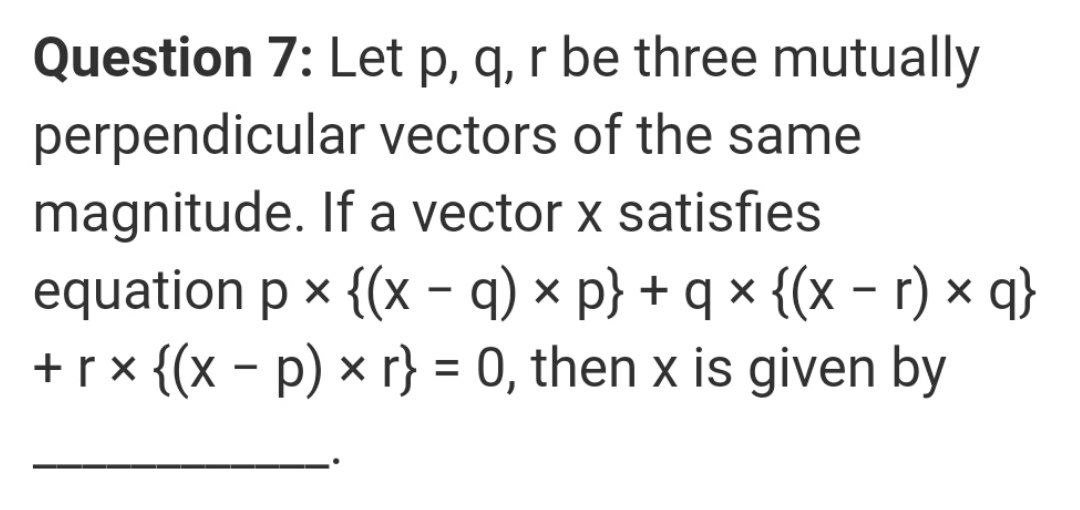
Answered Question 7 Let P Q R Be Three Bartleby

If X P And X Q Are The Factors Of X 2 Px Q Then The Values Of P And Q Are Respectively

If X Py Q X Y P Q Then D2y Dx2

Exercise 4 Label The Simple Proposition With The C Gauthmath

2

If X P Q P Q P Q P Q Then Find The Value Of Qx2 2px Q Brainly In

What Is The Value Of P And Q If The Polynomial Px 3 3x 2 9x Q Has The Factors X 2 And X 1 Quora

Jstor Org

Ijmttjournal Org

Jstor Org

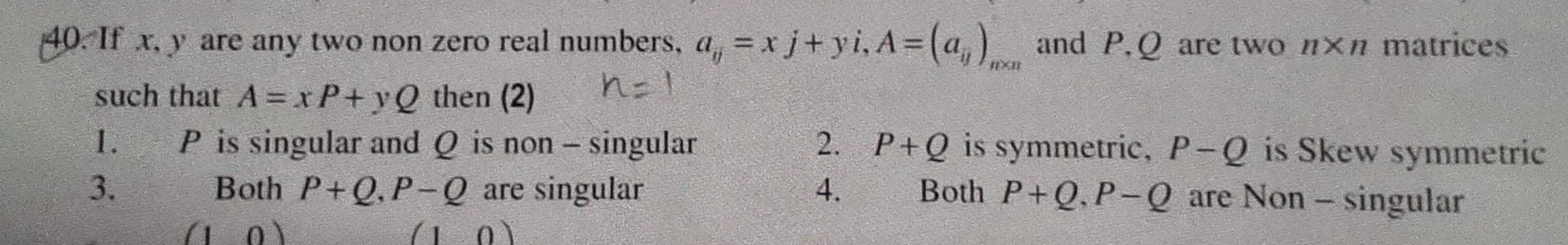
X 40 If X Y Are Any Two Non Zero Real Numbers A Math

If P And Q Are Distinct Reals Then 2 X P X Q P X P Q Q X Q P P Q 2 X P 2 X Q 2 Is Satisfied By A No Value Of X B Exactly One Value Of X C Exactly Two Value

Solved Let P Q R And S Be Subsets Of A Universal Set U Chegg Com

If X P Q P Q P Q P Q Then Find The Value Of Qx 2 2px Q Brainly In

If X 1 And X Minus 1 Of Factors Of P X Cube X Square 2 X Q Then Find The Value Of P And Q Brainly In

If X 8 1 3 5 1 2 10 1 4 And Y 2 1 1 0 2 1 5 P Q Then Find P Q If Y X 1 Sarthaks Econnect Largest Online Education Community

How To Solve The Question5x 2 A X P X Q P Q Quora

17 If X P Sec Q Q Tan Q And Y P Tan Q Q Sec Q Then Prove That X2 Y2 P2 Q2

If X P 0 X P Q Then P Haryana Ntse Stage 1 13 A Q Frac 1 Q Q Frac 1 A 1 B 1 C Q A D Snapsolve

Pdf A Completeness Proof For Bisimulation In The Pi Calculus Using Isabelle Semantic Scholar

If X Py Q X Y P Q Then D2y Dx2

Real Analysis Why Does X Q Leq X P Imply That Ell P Subset Ell Q Mathematics Stack Exchange

Core Ac Uk

23rd Ans Plz Q 23 If X P 2q P 2qp 2q P 2q Then Show That Qx2 Px Q 0 Maths Number Systems Meritnation Com

Chapter 2 The Logic Of Quantified Statements Section

Ml Aggarwal Solutions For Class 10 Chapter 5 Quadratic Equations In One Variable Free Pdf Available

1 Prove That The Empty Set Is A Subset Of Every Set Pdf Free Download

Let P And Q Be Real Numbers Such That P 0 P 3

Archive Ouverte Unige Ch

If X P 2q P 2q P 2q P 2q Then Show That Qx2 Px Q 0 Class 9 Chapter 1 Important Questions Youtube

If P Q Are The Roots Of Equation X 2 Px Q 0 Then Value Of P Must Be Equal To Youtube

Incoming Term: if x^p^q=(x^p)^q then p=, if x^py^q=(x+y)^p+q then dy/dx, if x ^ p * y ^ q = (x + y) ^ (p + q) then prove that (dy)/(dx) = y/x,