√ダウンロード 三 平方 の 定理 難問 922242

無料 中３数学 発展 応用問題 解答プリント 334 三平方の定理２

 以下の図のようになるのでしょうか。 先に結論を紹介すると「 なります 」。 なぜなら三平方の定理から次のことが成立するからです。 （ 2 倍× 2 ） 2 ＝（ 2 倍×√3） 2 ＋（ 2 倍× 1 ） 2 これを展開すると、このようになります。 16 ＝ 12 ＋ 4 では 2 倍 適切な 中 3 数学 三 平方 の 定理 高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料 中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中3数学 三平方の定理 で最も重要なポイントとは 映像授業の

三 平方 の 定理 難問

三 平方 の 定理 難問-三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し50 グレア 三 平方 の 定理 難問 円の中の図形の問題で三平方の定理を使う問題です 中学数学に関する 高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料 Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor

三平方の定理の応用

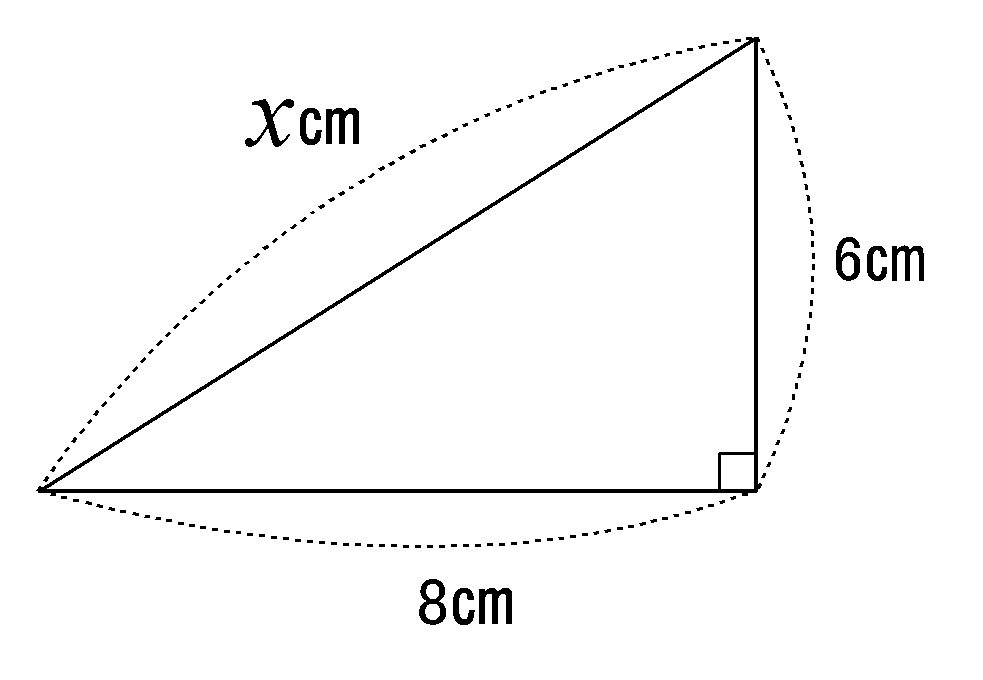
 三平方の定理を利用する難問 1辺が 2 2 の正六角形の中心に点Oを取り、その真上の点をPとする。 正六角形の各頂点からPまでの長さを 6 6 とするとき、OPの長さを求めよ ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこ三角数定理 三つの平方数の和 三角数かつ平方数（四角数）であるもの平方根 有理数と無理数 1 次の(あ)～(お)にあてはまる言葉を、①～⑤の中から選びなさい。 数 正の整数（ ） 0 2 次の①～⑤の中で、無理数であるものを選びなさい。 324 ① 自然数 ② 有理数 ③ 分数 ④ 無理数 ⑤ 負の整数

三平方の定理難問 中3数学 実力テスト用 高校入試過去問改 『三平方の定理① 中3数学 3学期期末テスト用 教科書178－1㌻』 中学3年 数学 東京書籍 三平方の定理 教科書練習問題 三平方の定理 三平方の定理の逆 三平方の定理の利用中3数学｜赤城の裾野三平方の定理 発展問題まとめ お疲れ様でした！ 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが中3 数学 1式の計算 2平方根 32次方程式 3中点連結定理の利用 5発展三角形の重心の利用 1三平方の定理(基本) 10発展相似比と面積比 1拡大図と縮図 新指導要領の範囲外 円 (web版は「追加講義」に掲載) 5相似 6図形の比 7三平方の定理 中3数学 Title E786C73> Author watabe 中 3 数学 三 平方 の 定理 中

三 平方 の 定理 難問のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	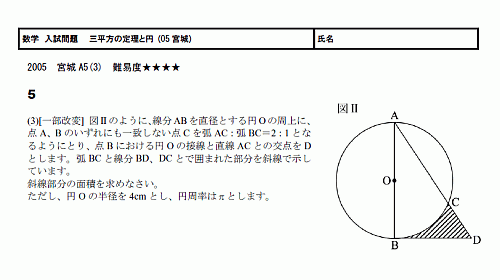1	1
1	1	1
1	1	1
1	1	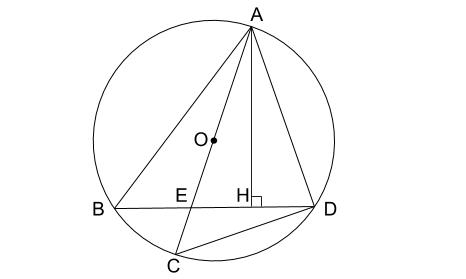1
1	1	1
1	1	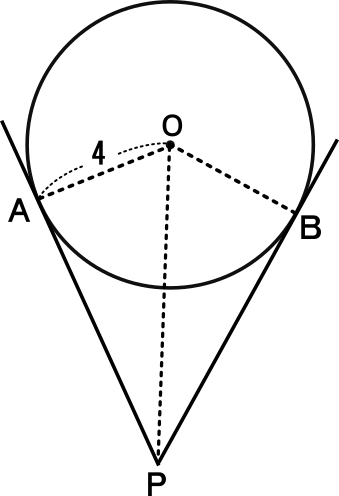1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1	1
1	1

 中学数学難問三平方の定理解き方数問ですが、一問だけでもいいのでよろしくお願いします また becは二等辺三角形だから ∠ebc=∠ecb ゆえに、eb=ec これらを使って aceに対して3平方の定理を使うことでecを求めることが出来ます。 息子の中学三年生 画像をダウンロード 三 平方 の 定理 難問 それで、三平方の定理を使えば、 2× 2 ＝√3×√3＋ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度